MiniMax – Game Theory

Minimax — is a decision rule used in decision theory, game theory, statistics and philosophy for minimizing the possible loss for a worst case (maximum loss) scenario.

This article will be a bit different from previous ones which are based on some new technologies to use in your projects.

Interesting? I will describe Minimax algorithm from the perspective of Game theory. Just letting you know what you are to expect:

• So what’s Minimax algorithm?
• Plan and code
• Algorithm description
• Optimizations
• Deepness optimization
• Alpha-Beta optimization
• Advice
• Conclusion

For coding, we will use language Objective-C.Don’t worry though, there will be more theory than just code.

The direction is set, let’s go.

So what’s Minimax algorithm?

Minimax — is a decision rule used in decision theory, game theory, statistics and philosophy for minimizing the possible loss for a worst case (maximum loss) scenario. Originally formulated for two-player zero-sum game theory, covering both the cases where players take alternate moves and those where they make simultaneous moves, it has also been extended to more complex games and to general decision-making in the presence of uncertainty.

Coooooooooool!

Now that we have the definition, what logic is embedded in it? Let’s suggest that you are playing a game against your friend. And then each step you take you, want to maximize your win and your friend also wants to minimize his loss. Eventually, it’s the same definition for both of you. Your next decision should be maximizing your current win position knowing that your friend in the next step will minimize his loss position and knowing that the next step you will also maximize your win position…

Catching this recursion smell? So the main idea of this algorithm is to make the best decision knowing that your opponent will do the same.

We will build this algorithm using tree representation. Each new generation of children is possible the next step of another player. For example, the first generation is your possible steps, each step will lead to some list of the opponent’s possible steps. In this situation, your step is the “father vertex” and possible next steps of your opponent are it’s “children vertexes”.

Here is the final algorithm code with all optimizations.

#pragma mark – Public

– (NSUInteger)startAlgorithmWithAITurn:(BOOL)aiTurn; {

return [self alphabetaAlgorithm:_searchingDeapthalpha:NSIntegerMin beta:NSIntegerMax maximizing:aiTurn];

}

#pragma mark – Private

– (NSInteger)alphabetaAlgorithm:(NSInteger)depth alpha:(NSInteger)alpha beta:(NSInteger)beta maximizing:(BOOL)maximizing {

self.currentCheckingDepth = _searchingDeapth – depth;

if (self.datasource == nil || self.delegate == nil) {

return 0;

}

if (depth == 0 || [self.datasource checkStopConditionForAlgorithm:self onAITurn:maximizing]) {

return [self.datasource evaluateForAlgorithm:selfonAITurn:maximizing];

}

NSArray *nextStates = [self.datasourcepossibleNextStatesForAlgorithm:self onAITurn:maximizing];

for (id state in nextStates) {

[self.delegate performActionForAlgorithm:self andState:state onAITurn:maximizing];

if (maximizing) {

alpha = MAX(alpha, [self alphabetaAlgorithm:depth – 1 alpha:alpha beta:beta maximizing:NO]);

} else {

beta = MIN(beta, [self alphabetaAlgorithm:depth – 1alpha:alpha beta:beta maximizing:YES]);

}

[self.delegate undoActionForAlgorithm:self andState:state onAITurn:maximizing];

if (beta <= alpha) {

break;

}

}

return (maximizing ? alpha : beta);

}

Algorithm description

Let’s close our eyes on optimizations and start with the initial things that we need. First of all, we need an algorithm that will give back the list of possible next steps based on a made step. We use this to produce other children vertexes as described previously.

Secondly, we need an algorithm that will calculate evaluation of the game result at the end of the game. Each vertex(made step) will have assigned value with the evaluated result using this algorithm. How it will be assigned will be described later.

So how does this work using a tree and these algorithms? Logically algorithm is divided into two parts:

1. Our turn

2. Opponents turn

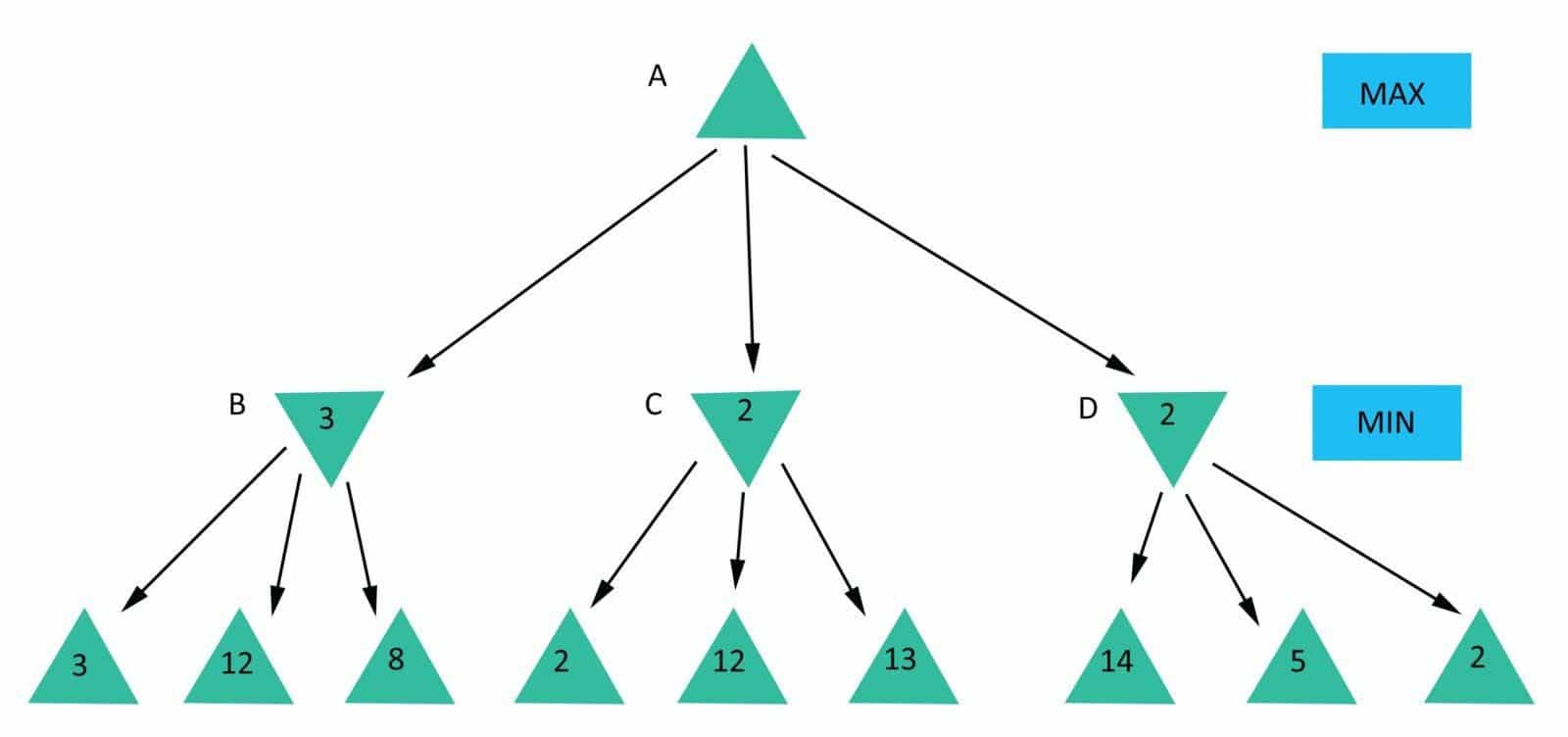
On “our turn” as next vertex, we choose one of our children that have the best evaluation value. Then as next chosen step generates possible opponents steps with its evaluation, he will choose worst evaluation value(worst for us means best for him).

This simply means that we will take the maximum evaluated step from possible opponents steps and the opponent will take the minimum evaluated step from our possible next steps.

The Next question is — when will we evaluate step? The first thing that comes to mind — just when it’s created. But hold on a minute, how can we calculate it immediately if it depends on the next generation, or in other words on another player’s step? It means that our step value will be maximum from the next generation step value, which is an opponent step. From another point of view, opponents step value will be minimum from the next generation step values, which is mine.

Following this rule, we can say that evaluation will be made when the game ends, as it’s final generation of steps. After that, it will unwind in back direction marking all vertexes with previously described calculated value until it gets to the root.

Recursive generation ends if:

• We get a winner
• It’s not possible to have the next move, we get a draw
• Evaluation of game state can be calculated in a next way:
• If we win, then evaluated value should be bigger than some positive value
• If we lose, then it should be lower than some negative value
• If we have a draw then it should be in between this values
• It means that the better position we have, the bigger value it should be.

This evaluation may depend on different things. Let’s take for example that for evaluation, we give it a situation where we are winners.

Then it may evaluate depending on next values:

1. How much steps I took to get the win

2. How close was your opponent to the win

etc…

This function is one of the most important parts of the algorithm. The better organized it is, the better results you get. A function that depends only on one characteristic will not be as accurate as a function that depends on ten. Also, characteristics you choose for evaluation should have logical meaning. If you will treat that evaluation value is bigger because the player is a woman other than a man, it makes some sense for the sexists but not for the algorithm. As a result, you will receive wrong results. And everything is because you’re a sexist.

Great!, now we generally understand the algorithm and what idea lays under it. Sound cool, but still, it’s not as good when it comes to execution time. Why?

Optimizations

For usage, for example, let’s select “four in a row” game. If you don’t know what it is, here is a short description:

“It is the goal of the game to connect four of your tokens in a line. All directions (vertical, horizontal, diagonal) are allowed. Players take turns putting one of their tokens into one of the seven slots. A token falls down as far as possible within a slot. The player with the red tokens begins. The game ends immediately when the first player connects four stones.”

Let’s think how our algorithm will work in this case. The field has 7*6=42 steps. At the beginning, each user can make 7 different steps. What does this data give to us? These values are worst ever. To make them more real, let’s say, for instance, that game will end in 30 steps and averagely user will have a possibility to select 5 rows. Using our algorithm we will get next approximate data. The first user can produce 5 steps; each step will produce 5 own steps. Now we’re having 5 + 25. These 25 steps, each can produce 5 new steps and that’s equal to 125. Which means on the third step of calculation we will have about155 steps. Each next step will produce more and more possible steps to follow. You can count them using the next function:

5¹ + 5² + 5³ + … + 5³⁰. This value is huge and a computer will take a lot of time to calculate so many steps.

Thankfully there are ready optimizations for Minimax algorithm, that will lower this value. We will talk about the two of them shortly.

Deepness optimization

Once upon a time, a very wise man said “why should we count it till the end? Can we make a decision somewhere in the middle?”. Yes, we can. Of course, in the end, accuracy will be much better than somewhere in the middle, but with a good algorithm for evaluation, we can lower this problem. So then what should we do, just add one more rule for “algorithm stops”. This rule is, to stop if current step deepness is on critical value. This value you can select on your own after some testing. I think with a bunch of tests you will find those that are matching your special situation. When we start evaluation based on this rule, we’re treating it as a draw.

This rule was not as hard, and can really optimize our algorithms. However still, it’s lowering our accuracy, and to make it work, we just can’t use super low deepness otherwise it will give us wrong, and non-accurate values. I will tell you next, we selected that deepness 8 is fine for us. Even though it was taking a lot of time to get its final result. Next optimization has no influence on accuracy and reduces algorithm time really good. Its name is Alpha Beta and it’s this thing that breaks my mind out.

Alpha-Beta optimization

It’s meaning is simple. The idea is next — no need to count next branches if we know that already founded branch will have a better result. It’s just a waste of resources. The idea is simple, what about implementation?

To count that, we need two other variables to be passed to the recursive algorithm.

1. Alpha — it’s representing evaluation value on maximizing part

2. Beta — it’s representing evaluation value on minimizing part

From previous parts, we understood that we have to go to the end of our tree and only then after can we evaluate our results. So the first evaluation will be made on the last vertex if we would always choose left vertex. After that evaluation process will start for its immediate vertex and will go on for all left vertexes till one of the possible ones end and so on and so forth.

Why am I telling you this? It’s all because of understanding how evaluating vertexes is crucial for this optimization.

To make it easier for us to imagine, let’s suppose that we’re on the maximizing turn. To us, it means that we’re counting Alpha value. This value is counted as a maximum of all evaluation values of his offsprings. At the same time when we’re counting Alpha(we’re on the maximizing process) we have a Beta value. Here, it represents a current Beta value of his parent. Great!, now we know what Alpha and Beta means in a specific time. To avoid misunderstanding, alpha is our current evaluation value and beta is current further evaluation value.

The last thing is optimization check. If Beta is lower or equal the Alpha we’re stopping evaluation for all next child.

The last thing is optimization check. If Beta is lower or equals to the Alpha we’re stopping evaluation for all next offsprings.

Why does it work? Because Beta already is smaller than Alpha — value of its offspring, at the same time Alpha is counted as a maximum of possible offspring values. It means that now evaluation value for our step can’t become lower than the current value. From another point of view, the Beta that we have now is a current evaluation value of our parent. From the idea that currently, we’re maximizing, we may understand that our Parent is minimizing which means that it will select a minimum of its current value and its offsprings calculated value.

Putting all of these together — because we know that our calculated value is higher than the parent value, we make a decision that it will not select us as its next possible step(it has a better offspring and that gives him lower value if it selects them). From that point of view doing the next calculation is ridiculous, because they will not change the final result. So we, as the parent-offspring, we stop all calculations and return the current value. Using this, our parent will compare us and the current best choice. By previously described logic it will select its current value.

Using this optimization, we may cut huge branches and save a lot of work that would do nothing to the final result.

Advice

Great!, now that we know two optimizations that will make our algorithm work faster, I would like to give you one advice. Usually, when a machine makes a choice, the real user need some time to decide what to do next. We can use this time to prepare for next the decision.

So when we make our choice, let’s continue to work for all possible user choices. What does this give to us?

1. Bunch of them are already calculated from previous user iteration.

2. By the time user will select his choice, we will go far ahead with our calculation. It will increase a deepness of our tree, in other words — accuracy.

In the end, when the user makes a choice, we can simply cut off all other branches that were not selected and only continue with selected one.

It’s great, but then let’s make a global conclusion on what I suppose — do not start your algorithm each time it’s your turn. Make it run once during the game and when a user selects some step, get calculated data for it and continue our calculation until the end.

Someone will say, that it’s has a heavy memory issue. Yes, it does, but this’s just an advice, you can combine two solutions to find what best fits your time, memory, and accuracy for your particular situation.

Also, I would recommend performing calculations for each possible step in a new thread, but it’s quite a different story.

Conclusion

Where should you use this information? Anywhere you have to make or do decision-based on user action. Most often it might be games, but then, you can use your fantasy to integrate it in a place where you would have to reflect on any performed action. The only thing you need to understand is the algorithm for two parts that are “playing” against each other.

The end!